Message-Passing Algorithms and Homology
In the following pages, still under construction, one shall find supplementary material to the dissertation.
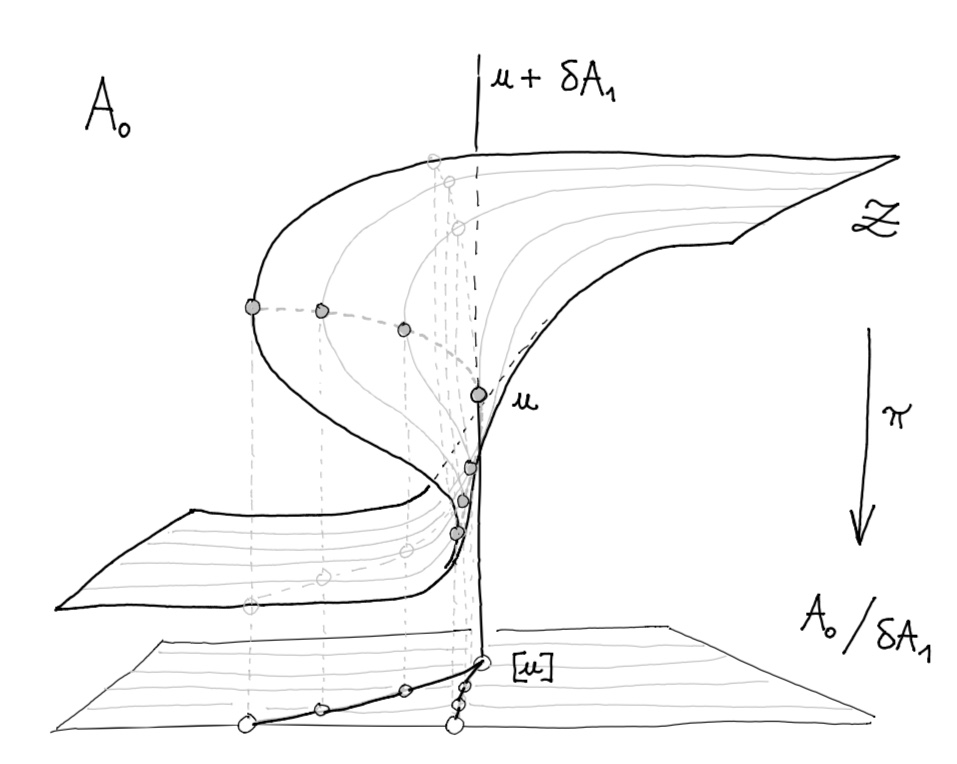
1) This overview should take the reader to quickly understand what the above drawing represents:
- a collection of local interaction potentials $u \in A_0$,
- the associated global hamiltonian $H_\Omega = \sum_\alpha u_\alpha$, viewed as the homology class $[u] = u + \delta A_1$,
- the manifold of consistent potentials ${\cal Z} \subseteq A_0$, stationary under diffusion,
Message passing algorithms explore a homology class of the form $[h] = h + \delta A_1$, until they eventually find a consistent potential $u \in [h] \cap {\cal Z}$.
2) It may occur that this intersection is not transverse, and instead consists of multiple homologous equilibria. The cusp depicted above illustrates the kind of singularities message-passing algorithms may encounter.
This geometric insight on message-passing equilibria allowed us to parameterise all singular states occuring on a graph with two loops, a cuspidal situation as illustrated above.